Cryptographic Tools for Non-Existence in the Domain Name System: NSEC and NSEC3

This is the second in a multi-part blog series on cryptography and the Domain Name System (DNS).

In my previous post, I described the first broad scale deployment of cryptography in the DNS, known as the Domain Name System Security Extensions (DNSSEC). I described how a name server can enable a requester to validate the correctness of a “positive” response to a query — when a queried domain name exists — by adding a digital signature to the DNS response returned.

The designers of DNSSEC, as well as academic researchers, have separately considered the answer of “negative” responses – when the domain name doesn’t exist. In this case, as I’ll explain, responding with a signed “does not exist” is not the best design. This makes the non-existence case interesting from a cryptographer’s perspective as well.

Initial Attempts

Consider a domain name like example.arpa that doesn’t exist.

If it did exist, then as I described in my previous post, the second-level domain (SLD) server for example.arpa would return a response signed by example.arpa’s zone signing key (ZSK).

So a first try for the case that the domain name doesn’t exist is for the SLD server to return the response “example.arpa doesn’t exist,” signed by example.arpa’s ZSK.

However, if example.arpa doesn’t exist, then example.arpa won’t have either an SLD server or a ZSK to sign with. So, this approach won’t work.

A second try is for the parent name server — the .arpa top-level domain (TLD) server in the example — to return the response “example.arpa doesn’t exist,” signed by the parent’s ZSK.

This could work if the .arpa DNS server knows the ZSK for .arpa. However, for security and performance reasons, the design preference for DNSSEC has been to keep private keys offline, within the zone’s provisioning system.

The provisioning system can precompute statements about domain names that do exist — but not about every possible individual domain name that doesn’t exist. So, this won’t work either, at least not for the servers that keep their private keys offline.

The third try is the design that DNSSEC settled on. The parent name server returns a “range statement,” previously signed with the ZSK, that states that there are no domain names in an ordered sequence between two “endpoints” where the endpoints depend on domain names that do exist. The range statements can therefore be signed offline, and yet the name server can still choose an appropriate signed response to return, based on the (non-existent) domain name in the query.

The DNS community has considered several approaches to constructing range statements, and they have varying cryptographic properties. Below I’ve described two such approaches. For simplicity, I’ve focused just on the basics in the discussion that follows. The astute reader will recognize that there are many more details involved both in the specification and the implementation of these techniques.

NSEC

The first approach, called NSEC, involved no additional cryptography beyond the DNSSEC signature on the range statement. In NSEC, the endpoints are actual domain names that exist. NSEC stands for “Next Secure,” referring to the fact that the second endpoint in the range is the “next” existing domain name following the first endpoint.

The NSEC resource record is documented in one of the original DNSSEC specifications, RFC4033, which was co-authored by Verisign.

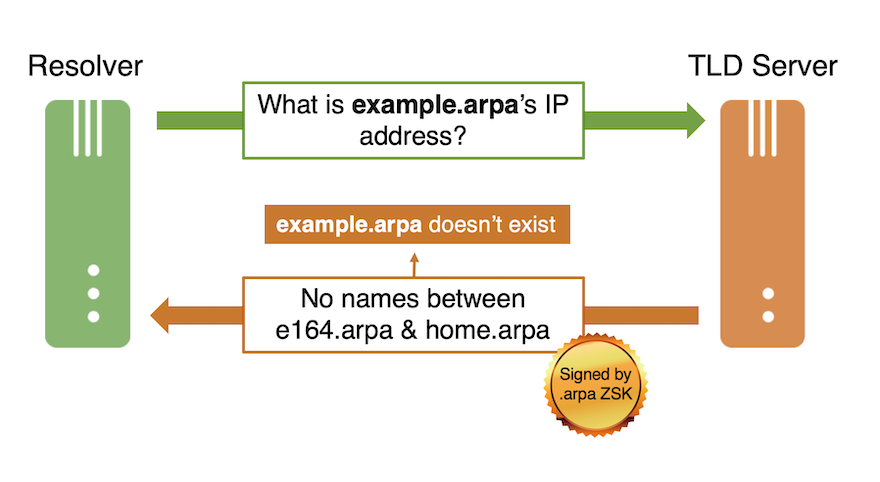
The .arpa zone implements NSEC. When the .arpa server receives the request “What is the IP address of example.arpa,” it returns the response “There are no names between e164.arpa and home.arpa.” This exchange is shown in the figure below and is analyzed in the associated DNSviz graph. (The response is accurate as of the writing of this post; it could be different in the future if names were added to or removed from the .arpa zone.)

NSEC has a side effect: responses immediately reveal unqueried domain names in the zone. Depending on the sensitivity of the zone, this may be undesirable from the perspective of the minimum disclosure principle.

*Figure 1. An example of a NSEC proof of non-existence (as of the writing of this post)*.

NSEC3

A second approach, called NSEC3 reduces the disclosure risk somewhat by defining the endpoints as hashes of existing domain names. (NSEC3 is documented in RFC 5155, which was also co-authored by Verisign.)

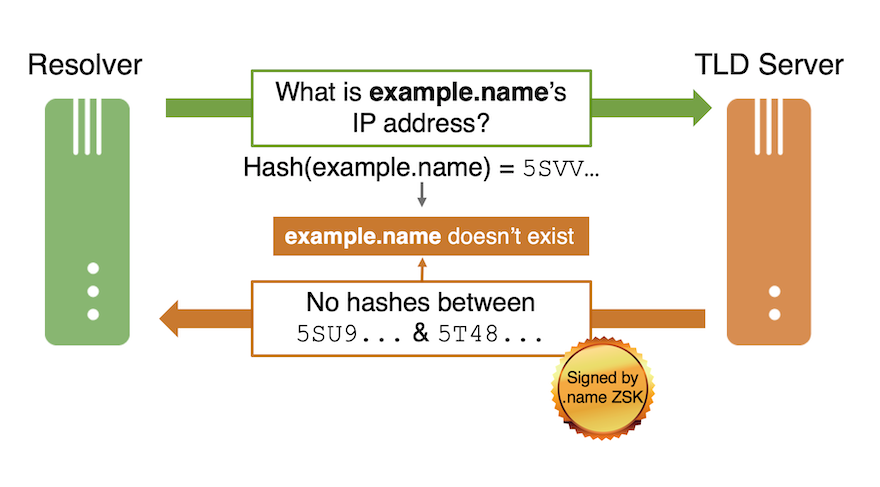
An example of NSEC3 can be seen with example.name, another domain that doesn’t exist. Here, the .name TLD server returns a range statement that “There are no domain names with hashes between 5SU9… and 5T48…”. Because the hash of example.name is “5SVV…” the response implies that “example.name” doesn’t exist.

This statement is shown in the figure below and in another DNSviz graph. (As above, the actual response could change if the .name zone changes.)

*Figure 2. An example of a NSEC3 proof of non-existence based on a hash function (as of the writing of this post)*.

To find out which domain name corresponds to one of the hashed endpoints, an adversary would have to do a trial-and-error or “dictionary” attack across multiple guesses of domain names, to see if any has a matching hash value. Such a search could be performed “offline,” i.e., without further interaction with the name server, which is why the disclosure risk is only somewhat reduced.

NSEC and NSEC3 are mutually exclusive. Nearly all TLDs, including all TLDs operated by Verisign, implement NSEC3. In addition to .arpa, the root zone also implements NSEC.

In my next post, I’ll describe NSEC5, an approach still in the experimental stage, that replaces the hash function in NSEC3 with a verifiable random function (VRF) to protect against offline dictionary attacks. I’ll also share some research Verisign Labs has done on a complementary approach that helps protect a client’s queries for non-existent domain names from disclosure.

Read the complete six blog series:

Initial Attempts

NSEC

NSEC3

You might also like